【答案】
(1)1020=1000×(1+4%×5)/(1+i)3
解得,i=5.57%
借款的半年利率为3%,则有:
年有效利率=(1+r/m)m-1=(1+3%)2-1=6.09%
由于投资国债的收益率小于借款的年有效利率,所以应该提前偿还借款。
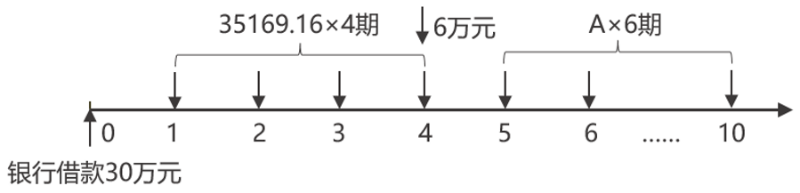
(2)当前每期还款额=300000/(P/A,3%,10)=35169.16(元)
设还款后每期还款额为A元,则
方法一:根据“流入的现值=流出的现值”:
300000=35169.16×(P/A,3%,4)+60000×(P/F,3%,4)+A×(P/A,3%,6)×(P/F,3%,4)
解得,A=24092.73(元)
方法二:最后6年还款额会减少,是因为提前还款6万元,换言之,若将第4年视为0时点,未来6年中还款额减少的现值=6万元,即
35169.16×(P/A,3%,6)-A×(P/A,3%,6)=60000
解得:A=24093.33(元)——计算方法的不同引起的小数尾差。
【变形与提示】(1)每期还款额计算的原理分析
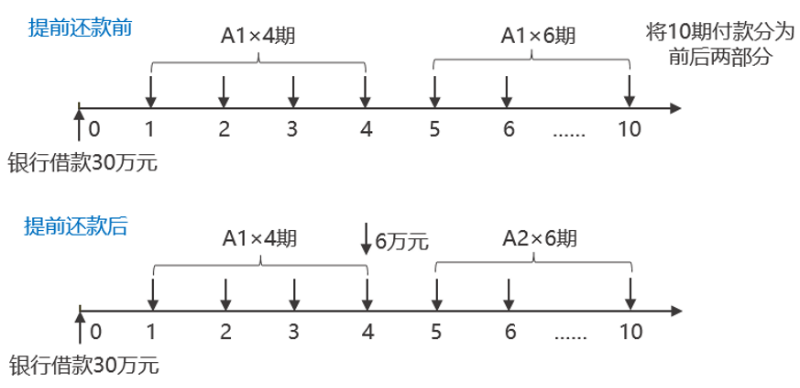
无论未来款项如何支付,小W最终归还款项的现值均为30万元。即
30=A1×(P/A,3%,4)+A1×(P/A,3%,6)×(P/F,3%,4)
=A1×(P/A,3%,4)+60000×(P/F,3%,4)+A2×(P/A,3%,6)×(P/F,3%,4)
可知,A1×(P/A,3%,6)×(P/F,3%,4)=60000×(P/F,3%,4)+A2×(P/A,3%,6)×(P/F,3%,4)
等号两边约掉(P/F,3%,4),可以得到:
A1×(P/A,3%,6)-A2×(P/A,3%,6)=60000——第2问中的方法二
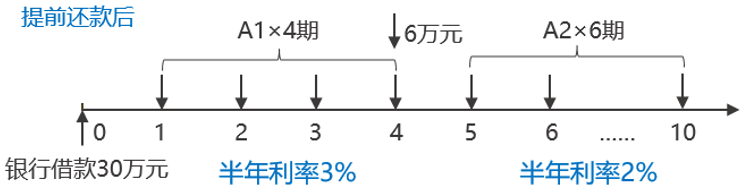
(2)利率变动分析。若提前偿还后,贷款利率降为每年4%,计算提前还款后的每期还款额。
300000=A1×(P/A,3%,4)+60000×(P/F,3%,4)+A2×(P/A,2%,6)×(P/F,3%,4),求解A2。
——折现率的选择:谁的地盘听谁的。
若使用方法二决策:
30=A1×(P/A,3%,4)+A1×(P/A,3%,6)×(P/F,3%,4)
=A1×(P/A,3%,4)+60000×(P/F,3%,4)+A2×(P/A,2%,6)×(P/F,3%,4)
可知,A1×(P/A,3%,6)×(P/F,3%,4)=60000×(P/F,3%,4)+A2×(P/A,2%,6)×(P/F,3%,4)
等号两边约掉(P/F,3%,4),可以得到:
A1×(P/A,3%,6)-A2×(P/A,2%,6)=60000——第2问中的方法二
易错点:A1、A2对应的年金现值系数中的折现率不同——A1是根据3%的折现率计算出来的。因此,在计算时推荐使用方法一。
(3)本题第1问考查到期一次还本付息(单利计息)+一年付息多次。
第2问考查“流入的现值=流出的现值”,倒算年金A。







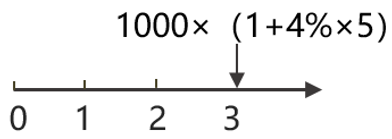





 津公网安备12010202000755号
津公网安备12010202000755号